Need for Speed – C++ versus Assembly Language

(originally published on codeproject.com)

Introduction

At first sight, we tend to believe that assembled code, i.e. machine code obtained from ASM (Assembly Language) source through an Assembler, should run faster than compiled code, i.e. machine code obtained from a High-Level Language source through a Compiler. The reason is that ASM has an almost one-to-one (isomorphic) mapping to machine code (ASM can be called symbolic machine code) while the Compiler works at least on a 2-stage process, the last one being a translation to ASM.
It used to be like that, but Compilers, in particular some C++ Compilers, are becoming increasingly ingenious at optimization and, in most cases, only very talented ASM programmers can equal them or do better. As always, there are many exceptions to the rule, but we will not elaborate on them here. A single example, tasks that deal with vectorized SIMD instructions are, at this time, better handled using ASM, although intrinsics (which are actually ASM in disguise) do the job almost as well.
In spite of that, ASM continues to be an important programming language to learn, not only because exist tasks that need to be handled as close to the hardware as possible but mainly because it provides the sort of insight impossible to acquire through High-Level Language study and practice.

For illustration purposes, I will present a program that will make some lengthy computation, first by calling a C++ function then by calling a linked assembled ASM object file. By lengthy computation I mean a few seconds, although the program can be easily modified to take less or more time. I had not done any steps to improve the C++ code; the Compiler had to do its best with what was there. On the other hand, I undertook a few optimization steps with the ASM source code and was able to improve the assembled performance by more than 30%.

Background

Our program will calculate a determinant under the Cramer’s Rule, which is an explicit formula for the solution of a system of linear equations, with the same number of equations as unknowns.
Just consider that the calculation of determinants is central to the Cramer’s Rule – this shall be enough for our purpose and we will not spend more time with the Math behind.
The Cramer’s Rule is great for calculating determinants of small matrixes; however it becomes computationally very expensive for larger matrix sizes, because its time complexity is O(n.n!) – Calculating the determinant of a 13×13 matrix takes seconds, a 14×14 matrix will take minutes and be ready to wait one hour to know the determinant of a 15×15 matrix.

Using the code

1) How it was compiled?

The C++ source code was compiled with Visual Studio 2015. The Release build of the compilation has the following settings:
Maximize Speed, Use Streaming SIMD Extensions 2 (/arch:SSE2), Fast (/fp:fast) floating point model, Disable Security Check (/GS-), not Enable C++ Exception, No (/SAFESEH:NO) for Win32.

2) How it works

The program will calculate the determinant of a 13×13 matrix by using the Cramer’s Rule. Most of the time is spent doing recursion and looping. The recursion is required because the determinant of a matrix is calculated from the determinants of lower order matrixes (called “minors”), which are obtained by eliminating the top row and a column at a time. Lower order matrixes determinants, are calculated the same way, and so on. In our program, the recursion ends when we reach a 4×4 matrix, whose determinant is then calculated directly. Matrixes of order 4×4, 3×3 and 2×2 have their determinants calculated directly and don’t do any recursion. The program loops through three levels to prepare the minor matrixes. For a 13×13 matrix the outer loop will execute 321,408,685 times, the middle loop 1,359,245,472 times and the innermost loop will execute 7,191,246,668 times.
The calculation of 4×4 minor determinants executes comparatively much fewer times, only 259,459,200.

3) Preparing the matrix

The matrix is populated with random float numbers in the range -50.0 to +50.0 rounded to 1 decimal place.

int i, j;
int numRows, numCols;
float *inMat;

srand(time(NULL));
numRows = 13; /*Change as you like for other matrix orders */
numCols = numRows;
inMat = (float*)malloc(numRows*numCols * sizeof(float));
for (i = 0;i < numRows;i++)
for (j = 0;j < numCols;j++)
/* Pointer to matrix, filled as one dimensional array */
inMat[i*numCols + j] = roundf((((float)rand() / (float)(RAND_MAX)) * 100 - 50) * 10) / 10;

printf("%dx%d Matrix\n\n", numRows, numCols);
printf("Input Matrix\n");
for (int i = 0; i < numRows; i++)
{
for (int j = 0; j < numCols; j++)
printf("%.1f\t", inMat[i*numCols + j]);
printf("\n");
}
printf("\n");

4) Measuring the time for the C++ execution:

void C_example(float* inMat, int rows)
{
LARGE_INTEGER frequency;
LARGE_INTEGER t1, t2;
double elapsedTime;

QueryPerformanceFrequency(&frequency);
QueryPerformanceCounter(&t1);
float det = determinant(inMat, rows);
QueryPerformanceCounter(&t2);
elapsedTime = (t2.QuadPart - t1.QuadPart) * 1000.0 / frequency.QuadPart;

printf("\nDeterminant of Matrix using C++ is %.2f.\n", det);
printf("Elapsed time: %f miliseconds\n", elapsedTime);
}

5) Calculating the determinant in C++:

float determinant(float*inMat, int rows)
{
HANDLE heapPtr;
float* minorMat;
int i, j, k, s;
float det = 0.0f, sign = 1.0f;

if (4 == rows)
{
/*
float A11 = inMat[0];
float A12 = inMat[1];
float A13 = inMat[2];
float A14 = inMat[3];
float A21 = inMat[rows];
float A22 = inMat[rows + 1];
float A23 = inMat[rows + 2];
float A24 = inMat[rows + 3];
float A31 = inMat[rows * 2];
float A32 = inMat[rows * 2 + 1];
float A33 = inMat[rows * 2 + 2];
float A34 = inMat[rows * 2 + 3];
float A41 = inMat[rows * 3];
float A42 = inMat[rows * 3 + 1];
float A43 = inMat[rows * 3 + 2];
float A44 = inMat[rows * 3 + 3];
(A13*A24-A14*A23) * ((A31*A42)-(A32*A41)) +
(A14*A22-A12*A24) * ((A31*A43)-(A33*A41)) +
(A13*A22-A12*A23) * ((A34*A41)-(A31*A44)) +
(A11*A24-A14*A21) * ((A32*A43)-(A33*A42)) +
(A11*A23-A13*A21) * ((A34*A42)-(A32*A44)) +
(A11*A22-A12*A21) * ((A33*A44)-(A34*A43))
*/
det = (inMat[2] * inMat[rows + 3] - inMat[3] * inMat[rows + 2]) * ((inMat[rows * 2] * inMat[rows * 3 + 1]) - (inMat[rows * 2 + 1] * inMat[rows * 3])) +
(inMat[3] * inMat[rows + 1] - inMat[1] * inMat[rows + 3]) * ((inMat[rows * 2] * inMat[rows * 3 + 2]) - (inMat[rows * 2 + 2] * inMat[rows * 3])) +
(inMat[2] * inMat[rows + 1] - inMat[1] * inMat[rows + 2]) * ((inMat[rows * 2 + 3] * inMat[rows * 3]) - (inMat[rows * 2] *inMat[rows * 3 + 3])) +
(inMat[0] * inMat[rows + 3] - inMat[3] * inMat[rows]) * ((inMat[rows * 2 + 1] * inMat[rows * 3 + 2]) - (inMat[rows * 2 + 2] * inMat[rows * 3 + 1])) +
(inMat[0] * inMat[rows + 2] - inMat[2] * inMat[rows]) * ((inMat[rows * 2 + 3] * inMat[rows * 3 + 1]) - (inMat[rows * 2 + 1] * inMat[rows * 3 + 3])) +
(inMat[0] * inMat[rows + 1] - inMat[1] * inMat[rows]) * ((inMat[rows * 2 + 2] * inMat[rows * 3 + 3]) - (inMat[rows * 2 + 3] * inMat[rows * 3 + 2]));
}
else if (3 == rows)
{
det = inMat[0] * (inMat[rows + 1] * inMat[rows * 2 + 2] - inMat[rows + 2] * inMat[rows * 2 + 1]) -
inMat[1] * (inMat[rows] * inMat[rows * 2 + 2] - inMat[rows + 2] * inMat[rows * 2]) +
inMat[2] * (inMat[rows] * inMat[rows * 2 + 1] - inMat[rows + 1] * inMat[rows * 2]);
}
else if (2 == rows)
{
det = inMat[0] * inMat[rows + 1] - inMat[1] * inMat[rows];
}

else
{
heapPtr = GetProcessHeap();
minorMat = (float*)HeapAlloc(heapPtr, 0, (rows - 1)*(rows - 1) * sizeof(float));
for (i = 0;i < rows;i++, sign *= -1)
{
for (j = 1;j < rows;j++)
{
for (s = k = 0;k < rows;k++)
{
if (i != k)
{
minorMat[((j - 1)*(rows - 1) + s)] = inMat[(j*rows + k)];
s++;
}
}
}

det += (sign * inMat[i] * determinant(minorMat, rows - 1));
}
HeapFree(heapPtr, 0, minorMat);
}

return det;
}

6) Measuring the assembled ASM execution time:

void Asm_Example(float* inMat, int rows)
{
LARGE_INTEGER frequency;
LARGE_INTEGER t1, t2;
double elapsedTime;

QueryPerformanceFrequency(&frequency);
QueryPerformanceCounter(&t1);
float det = Determinant(inMat, rows);
QueryPerformanceCounter(&t2);
elapsedTime = (t2.QuadPart - t1.QuadPart) * 1000.0 / frequency.QuadPart;

printf("\nDeterminant of Matrix using Asm is %.2f\n", det);
printf("Elapsed time: %f miliseconds\n", elapsedTime);
}

Note that the Determinant (with capital D) function is an external function:

extern "C"
{
float Determinant(void* intMat, size_t rows);
}

7) The ASM source code.

We have 3 variations of source code: 1 for 32-bit and 2 for 64-bit.
The 32-bit version can be assembled as is with MASM.
For the 64-bit, we have one version ready to be assembled with JWASM (or HJWASM, which is a recent evolution of the first). JWASM has at least the same features under 64-bit that MASM has under 32-bit. In other words, MASM 64-bit lacks some of its own 32-bit functionality, but it works well and has its fans who never stop developing macros to compensate the shortcomings (or not, actually MASM means “macro assembler”, so it’s in the name what you are expected to do!). Either way, I made as well a version that can be assembled with MASM 64-bit.

Below is the 64-bit version for JWASM/HJWASM (the 32-bit and the MASM 64-bit versions can be downloaded from below):

option casemap:none
option frame:auto

_MM_SHUFFLE MACRO fp3, fp2, fp1, fp0
exitm <( ( ( fp3 ) shl 6) or ( ( fp2 ) shl 4 ) or ( ( fp1 ) shl 2 ) or ( ( fp0 ) ) ) >
ENDM

_PERMUTE_PS MACRO v, c
shufps v, v, c
ENDM

_VECTORSWIZZLE MACRO v, fp0, fp1, fp2, fp3
_PERMUTE_PS v, _MM_SHUFFLE (fp3, fp2, fp1, fp0)
ENDM

_REALSTOXMM MACRO par1, par2, par3, par4
Local xmmValue
.const
align 16
xmmValue dd par1, par2, par3, par4
.code
exitm
ENDM

T4x4MATRIX struct 16
r0 XMMWORD ?
r1 XMMWORD ?
r2 XMMWORD ?
r3 XMMWORD ?
T4x4MATRIX ends

TFLOAT3X3 struct 4
r0 REAL4 3 dup (?)
r1 REAL4 3 dup (?)
r2 REAL4 3 dup (?)
TFLOAT3X3 ends

HANDLE TYPEDEF PTR
HeapAlloc proto :HANDLE, : DWORD, :QWORD
HeapFree proto :HANDLE, : DWORD, : PTR
GetProcessHeap proto

.const
_MINUSONE REAL4 -1.0

.code

RecursiveDetCalc proc private FRAME uses rsi rdi r12 r13 r14 inMat : ptr, rows : qword
LOCAL heapPtr : ptr
LOCAL det : REAL4
LOCAL sign : REAL4

.if rdx==4
ASSUME rcx : ptr T4x4MATRIX
movups xmm6, [rcx].r2
movups xmm1, [rcx].r3
movaps xmm2, xmm6
_VECTORSWIZZLE xmm2, 1, 0, 0, 0
movaps xmm3, xmm1
_VECTORSWIZZLE xmm3, 2, 2, 1, 1
movaps xmm4, xmm6
_VECTORSWIZZLE xmm4, 1, 0, 0, 0
movaps xmm5, xmm1
_VECTORSWIZZLE xmm5, 3, 3, 3, 2
movaps xmm0, xmm6
_VECTORSWIZZLE xmm0, 2, 2, 1, 1
movaps xmm7, xmm1
_VECTORSWIZZLE xmm7, 3, 3, 3, 2

mulps xmm2, xmm3
movaps xmm8, xmm2
mulps xmm4, xmm5
movaps xmm9, xmm4
mulps xmm0, xmm7
movaps xmm10, xmm0

movaps xmm2, xmm6
_VECTORSWIZZLE xmm2, 2, 2, 1, 1
movaps xmm3, xmm1
_VECTORSWIZZLE xmm3, 1, 0, 0, 0
movaps xmm4, xmm6
_VECTORSWIZZLE xmm4, 3, 3, 3, 2
movaps xmm5, xmm1
_VECTORSWIZZLE xmm5, 1, 0, 0, 0
movaps xmm0, xmm6
_VECTORSWIZZLE xmm0, 3, 3, 3, 2
movaps xmm7, xmm1
_VECTORSWIZZLE xmm7, 2, 2, 1, 1

mulps xmm2, xmm3
movaps xmm3, xmm8
subps xmm3, xmm2
movaps xmm8, xmm3

mulps xmm4, xmm5
subps xmm9, xmm4

mulps xmm0, xmm7
subps xmm10, xmm0

movups xmm6, [rcx].r1
movaps xmm2, xmm6
_VECTORSWIZZLE xmm2, 3, 3, 3, 2
movaps xmm3, xmm6
_VECTORSWIZZLE xmm3, 2, 2, 1, 1
movaps xmm4, xmm6
_VECTORSWIZZLE xmm4, 1, 0, 0, 0

movups xmm0, [rcx].r0
mulps xmm0, XMMWORD ptr _REALSTOXMM(1.0, -1.0, 1.0, -1.0)

mulps xmm2, xmm8

mulps xmm3, xmm9
subps xmm2, xmm3

mulps xmm4, xmm10
addps xmm4, xmm2

mulps xmm0, xmm4
shufps xmm4, xmm0, _MM_SHUFFLE(1,0,0,0)
addps xmm4, xmm0
shufps xmm0, xmm4, _MM_SHUFFLE(0,3,0,0)
addps xmm0, xmm4
_PERMUTE_PS xmm0, _MM_SHUFFLE(2,2,2,2)

ASSUME rcx : nothing
.elseif rdx==3 ; Only used for 3x3 matrixes
ASSUME rcx : ptr TFLOAT3X3
movups xmm3, XMMWORD ptr [rcx].r0
mulps xmm3, XMMWORD ptr _REALSTOXMM(1.0,-1.0,1.0,1.0)

movups xmm0, XMMWORD ptr [rcx].r1+4
movq xmm2, qword ptr [rcx].r2+4
shufps xmm0, xmm2, _MM_SHUFFLE(1,0,1,0)
;calculate first determinant
shufps xmm1, xmm0, _MM_SHUFFLE(0,1,0,0)
mulps xmm0, xmm1
shufps xmm1, xmm0, _MM_SHUFFLE(2,0,0,0)
shufps xmm0, xmm0, _MM_SHUFFLE(3,3,3,3)
shufps xmm1, xmm1, _MM_SHUFFLE(3,3,3,3)
subps xmm0, xmm1
movaps xmm4, xmm0

movups xmm0, XMMWORD ptr [rcx].r1
movups xmm2, XMMWORD ptr [rcx].r1+8
shufps xmm0, xmm2, _MM_SHUFFLE(3,1,2,0)
;calculate second determinant
shufps xmm1, xmm0, _MM_SHUFFLE(0,1,0,0)
mulps xmm0, xmm1
shufps xmm1, xmm0, _MM_SHUFFLE(2,0,0,0)
shufps xmm0, xmm0, _MM_SHUFFLE(3,3,3,3)
shufps xmm1, xmm1, _MM_SHUFFLE(3,3,3,3)
subps xmm0, xmm1
movaps xmm5, xmm0

movups xmm0, XMMWORD ptr [rcx].r1
movq xmm2, qword ptr [rcx].r2
shufps xmm0, xmm2, _MM_SHUFFLE(1,0,1,0)
;calculate third determinant
shufps xmm1, xmm0, _MM_SHUFFLE(0,1,0,0)
mulps xmm0, xmm1
shufps xmm1, xmm0, _MM_SHUFFLE(2,0,0,0)
shufps xmm0, xmm0, _MM_SHUFFLE(3,3,3,3)
shufps xmm1, xmm1, _MM_SHUFFLE(3,3,3,3)
subps xmm0, xmm1

unpckhps xmm4, xmm5
shufps xmm4, xmm0, _MM_SHUFFLE(0,0,1,0)
mulps xmm3, xmm4

movaps xmm0, xmm3
movhlps xmm0, xmm0
addps xmm0, xmm3
shufps xmm3, xmm3, 1
addss xmm0, xmm3
shufps xmm0, xmm0,0
ASSUME rcx : nothing
.elseif rdx==2 ; Only used for 2x2 matrixes
movss xmm0, dword ptr [rcx+12]
movss xmm1, dword ptr [rcx+8]
mulss xmm0, dword ptr [rcx]
mulss xmm1, dword ptr [rcx+4]
subss xmm0, xmm1
.else
mov rsi, rcx
mov rows, rdx
mov r13, rdx
mov det, 0.0
mov sign, 1.0; sign

INVOKE GetProcessHeap
mov heapPtr, rax
mov rax, rows
dec rax
mul rax
shl rax, 2
INVOKE HeapAlloc, heapPtr, 0, rax ; space for new (n-1)x(n-1) matrix
mov rdi, rax

mov r12,0
.while r12<r13
mov r10, 1
.while r10<r13
mov r11,0
mov r9,0

lea rax, [4*r13]
mul r10
mov r14, rax

lea rax, [4*r13-4]
lea rcx, [r10-1]
mul rcx
mov r8, rax

.while r11<r13
.if r12 != r11
lea rcx, [r14 + 4*r11]
mov eax, REAL4 ptr [rsi+rcx]
lea rcx, [r8+4*r9]
mov REAL4 ptr [rdi+rcx], eax
add r9, 1
.endif
add r11, 1
.endw
add r10, 1
.endw

lea rdx, [r13-1]
INVOKE RecursiveDetCalc, rdi, rdx

movss xmm1, dword ptr [rsi+4*r12]
mulss xmm1, sign
mulss xmm0, xmm1

addss xmm0, det

movss xmm1, sign
movss det, xmm0

mulss xmm1, _MINUSONE
movss sign, xmm1
add r12, 1
.endw
INVOKE HeapFree, heapPtr, 0, rdi
movss xmm0, det
.endif
ret
RecursiveDetCalc endp

Determinant proc public FRAME uses xmm6 xmm7 xmm8 xmm9 xmm10 inMat : ptr, rows : qword
; Save xmm registers here and do the calculation in the recursive function.

INVOKE RecursiveDetCalc, rcx, rdx
ret
Determinant endp

end

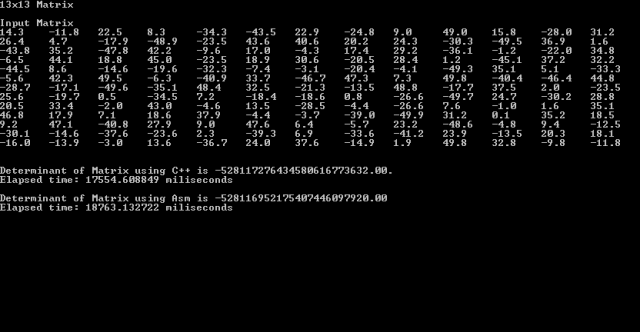
8) After compiling the 64-bit Release Build and running you will obtain results similar to the image below:

Disregard the difference in the determinant value, which is due to rounding errors under different variations of the calculation.

Why is ASM slower?

As mentioned, I made a number of optimizations to the ASM code but was not enough to beat the C++ compilation. The SIMD parts, namely the 4×4 minor determinants calculations are faster on the ASM code, but they do not weight that much in the total time taken by the whole.
I have seen the ASM listing produced by the C++ compiler and some parts are just mind blowing – nobody would believe a human would code that way (if he does the code would be almost impossible to maintain). The compiler uses every trick under the table in an automated way – difficult to beat. It knows about everything about how the pipelines and predictive branching work, it reorders of instructions, does loop tiling and uses cache-oblivious algorithms.

UPDATE 1

At the time of this writing, ASM programming still produces much faster code when compared with other programming languages or compilers. It is too early to claim that ASM programming is dead. I selected two popular languages and environments and replicated the C++ code.

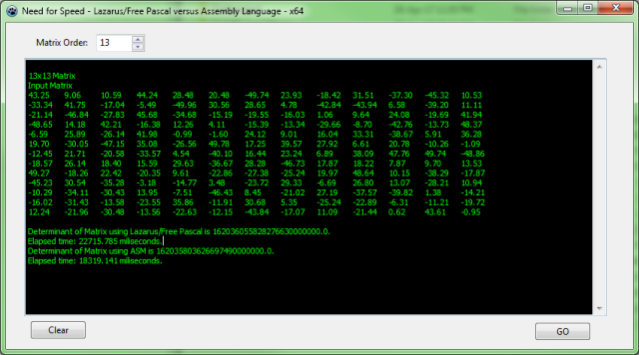
Lazarus/Free Pascal

Lazarus is an IDE that sports most RAD features of Delphi (old versions). Its integrated Free Pascal compiler appears to produce 64-bit executables a little faster than Delphi (although a little slower for 32-bit).
When compared with the Visual Studio C++ compiler, it lagged behind in our test, taking almost 30% more time.
For most applications this will not be a drama, as you know.

You can download the full Free Pascal source code for the test from below. There are a couple of points to mention.

For 32-bit, you need to assemble the ASM with JWASM/HJWASM (using the switch -zt0), not with MASM, in order to remove the STDCALL name mangling of the API calls (ex: _HeapAlloc@12). Free Pascal (and Delphi as well) are not able to tackle with that.
Unlike Delphi, Free Pascal is not able to handle the API references within the ASM code at link time without wrapper functions. This is an inconvenience, although does not reflect sensibly in the overall performance.

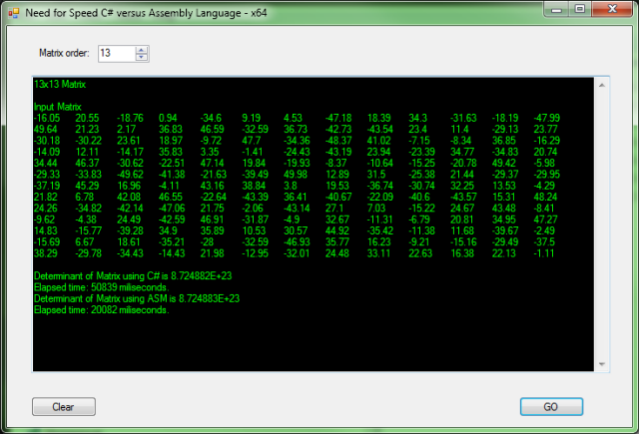
Visual Studio/C#

C# is a nice programming language invented by Microsoft. In its current implementation, it is heavily integrated with the huge .Net Framework and the huge Common Language Runtime.
Although C# has been performing faster and faster throughout the years, in our test the JIT compiler did not produce astonishing results on the speed department. I do believe the C# source can be improved for speed, no doubts about that, but also the C++ and Free Pascal can. So, don’t rush to take conclusions.

You can download from below the full C# source code for the test. As usual, the ASM is called through a C++ CLI class, otherwise we would need another DLL.

We have used VS 2015. You must build either for x64 or for x86 CPUs, not for Any Cpu.
You can build it as well as a single x86 or x64 executable (no DLL at all) through simple batch files, as shown in the directory CSharpSingleExe of your download. This is based in our article Mixing .NET and Assembly Language in a standalone 64-bit exe .

UPDATE 2

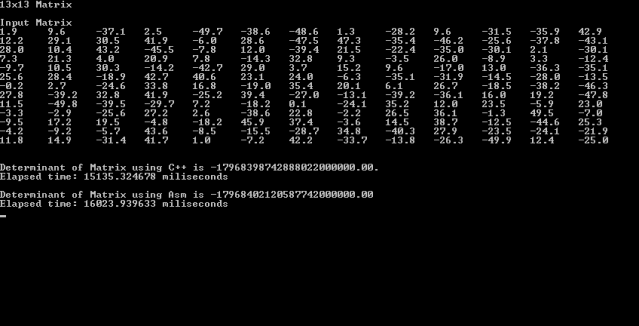
I decided to replicate the C++ versus ASM test without using heap memory, just stack memory.
The impact of heap allocation is real but not tantamount (about 16-18%) and affects both C++ and ASM in the (almost) same degree. The conclusion remains the same – as expected – but the test is now more transparent. The changed code can be downloaded from below (CalcDetStackMem.zip).

Update History

18 Apr 2017 – Initial Article
28 Apr 2017 – Included equivalent tests for Free Pascal and C#. Small fixes in the ASM for both x86 and x64.
5 May 2017 – C++ versus ASM test using Stack instead of Heap memory allocation.